ÉTAPE sur 2 Parmi les 4 propositions suivantes, préciser celle qui semble être la plus pertinente pour répondre à la question posée.
Compléter les seules informations qui permettent de résoudre la problématique : (Les cases qui ne vous semblent pas pertinentes doivent prendre la valeur 0.) -
 Le calcul du quotient doit être arrondi à 10 -4.
ÉTAPE sur 2 Conclusion : La durée du placement doit donc être de
années.
4. Tableau d'amortissement
ÉTAPE sur 6 Étude des mensualités maximum pour ce couple. - Calculer les revenus mensuels :
€
- Déterminer la mensualité maximum :
€
- Le revenu mensuel du couple est de €.
- La mensualité maximum est de €.
Le banquier réalise l'offre suivante : - OFFRE : Un remboursement sur ans aux taux annuel de % permet d'emprunter €.
Calculer le taux mensuel : tm =
ÉTAPE sur 6 Compléter à 0.01 près le tableau d'amortissement suivant : | Période | Capital en € | Intérêt en € | Amortissement en € | Mensualité en € |  | Montant emprunté
ou
Capital restant dû = Capital
Amortissement | Capital 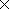 tm tm | Mensualité
Intérêt | Mensualité en € | | 1ermois |
|
|
|
|
- Le taux mensuel est : tm =
Le banquier réalise l'offre suivante : - OFFRE : Un remboursement sur ans aux taux annuel de % permet d'emprunter €.
ÉTAPE sur 6 Compléter à 0.01 près le tableau d'amortissement suivant : | Période | Capital en € | Intérêt en € | Amortissement en € | Mensualité en € |  | Montant emprunté
ou
Capital restant dû = Capital
Amortissement | Capital 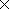 tm tm | Mensualité
Intérêt | Mensualité en € | | 1ermois | | | | | | 2emois |
|
|
|
|
- Le taux mensuel est : tm =
Le banquier réalise l'offre suivante : - OFFRE : Un remboursement sur ans aux taux annuel de % permet d'emprunter €.
ÉTAPE sur 6 Compléter à 0.01 près le tableau d'amortissement suivant : | Période | Capital en € | Intérêt en € | Amortissement en € | Mensualité en € |  | Montant emprunté
ou
Capital restant dû = Capital
Amortissement | Capital 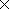 tm tm | Mensualité
Intérêt | Mensualité en € | | 1ermois | | | | | | 2emois | | | | | | 3emois |
|
|
|
|
- Le taux mensuel est : tm =
Le banquier réalise l'offre suivante : - OFFRE : Un remboursement sur ans aux taux annuel de % permet d'emprunter €
ÉTAPE sur 6 Pour compléter à 0.01 près le tableau d'amortissement suivant, vous devez réaliser ce tableau avec un tableur : | Période | Capital en € | Intérêt en € | Amortissement en € | Mensualité en € |  | Montant emprunté
ou
Capital restant dû = Capital
Amortissement | Capital 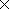 tm tm | Mensualité
Intérêt | Mensualité en € | | 1ermois | | | | | | 2emois | | | | | | 3emois | | | | | | ...emois | ... | ... | ... | ... | | emois |
|
|
|
| Au bout de ans, vous percevez la moitié de la somme empruntée. Pouvez-vous rembourser votre crédit ? Conclusion : Au début du crédit, on rembourse essentiellement des
.
- Le taux mensuel est : tm =
Le banquier réalise l'offre suivante : - OFFRE : Un remboursement sur ans aux taux annuel de % permet d'emprunter €.
ÉTAPE sur 6 Pour compléter à 0.01 près le tableau d'amortissement suivant, trouver la colonne qui se comporte comme une suite : On définit ainsi une suite
de premier terme
=
et de raison
. Les quatre formules sur les suites sont données ci-desous : Pour une suite arithmétique, la relation est donnée par :
| | Pour une suite géométrique, la relation est donnée par :
| | | |
Amortissement | Capital 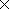 tm tm | Mensualité
Intérêt | Mensualité en € | | 1ermois | | | | | | 2emois | | | | | | 3emois | | | | | | ...emois | ... | ... | ... | ... | | emois | | | | | | ...emois | ... | ... | ... | ... | | emois |
|
|
|
| Calculer la somme de tous les termes de cette suite géométrique. Arrondir à l'unité. U1+ ... +U =
Conclusion : Le résultat précédent correspond au Le total des sommes versées à la banque est de :
€.
Le coût d'ensemble du crédit est de :
€.
2. Capitaliste Financier Versus Travail
ÉTAPE sur 3 Parmi les 2 entreprises, quelle est celle qui vous paraît la plus rentable ?
Votre réponse précédente est fausse. En effet on ne peut pas conclure sans réaliser des calculs.
Votre réponse précédente est juste.
ÉTAPE sur 3 Étudier l'évolution des bénéfices les 3 premiers mois. | Monsieur BANK | Monsieur WORK | - Calculer le taux mensuel : tm =
%
- Donner la valeur du capital placé : Ca0=
- Calculer le capital acquis le premier mois : Ca1 =
- Calculer le capital acquis le deuxième mois : Ca2 =
- Calculer le capital acquis le troisième mois : Ca3 =
On définit ainsi une suite
de premier terme
et de raison
. | - Déterminer la valeur du bénéfice mensuel : Bm =
- Donner la valeur du capital placé : Ca0=
- Calculer le capital acquis le premier mois : Ca1 =
- Calculer le capital acquis le deuxième mois : Ca2 =
- Calculer le capital acquis le troisième mois : Ca3 =
On définit ainsi une suite
de premier terme
et de raison
. |
Durée de la basse saison
en mois | Capital avec les intérêts
pour la société BANK
en € | Capital avec les bénéfices mensuels
pour la société WORK
en € | | 0 | | | | 1 | | | | 2 | | | | 3 | | | | ... | ... | ... | | 8 | ... | ... | - Les bénéfices de Monsieur BANK forme bien une suite géométrique de premier terme
= et de raison q=
- Les bénéfices de Monsieur WORK forme bien une suite arithmétique de premier terme
= et de raison r=
Regarder la vidéo pour construire un tableur : Les quatre formules sur les suites sont données ci-desous : Pour une suite arithmétique, la relation est donnée par :
| | Pour une suite géométrique, la relation est donnée par :
| | | |
Pour l'entreprise WORK U8=
En déduire le bénéfice annuel de chaque entreprise. - Bénéfice de l'entreprise BANK =
- Bénéfice de l'entreprise WORK =
Conclusion : Quel est le commerce le plus rentable ?
3. Paquet de cigarettes
?
ÉTAPE sur 2 Étudier l'évolution des montants des intérêts sur les 3 derniers mois. - Calculer le montant placé chaque mois : Mensualité =
€
- Calculer le taux mensuel : tm =
%
- Calculer la durée du placement en année : Durée=
- Calculer la durée du placement en mois : Durée=
| Durée du placement en mois | Capital avec les intérêts en € | | e versement | 0 |
| | e versement | 1 |
| | e versement | 2 |
| | ...e versement | ... | | | 3e versement | | | | 2e versement | | | | 1er versement | | | On définit ainsi une suite
de premier terme
=
et de raison
.
| Durée du placement en mois | Capital avec les intérêts en € | | e versement | 0 | | | e versement | 1 | | | e versement | 2 | | | ...e versement | ... | | | 3e versement | | | | 2e versement | | | | 1er versement | | | - Les sommes d'argent ainsi placées forment une suite géométrique de premier terme
= et de raison q=
Les quatre formules sur les suites sont données ci-desous : Pour une suite arithmétique, la relation est donnée par :
| | Pour une suite géométrique, la relation est donnée par :
| | | |
Conclusion : L'arrêt du tabac a rapporté la somme de
€ en ans.
1. Passage des intérêts simples aux intérêts composés
Les intérêts simples sont donnés par la relation suivante :
€. Le taux annuel est de
. la valeur attendue ne doit pas être exprimée en pourcentage. La Durée du placement de la première année est de
an. En utilisant la formule, déterminer les intérêts de la première année : I=
€ la valeur attendue ne doit pas être exprimée en pourcentage. La Durée du placement de la première année est de
an. En utilisant la formule, déterminer les intérêts de la première année : I=
€
En déduire le capital à la fin de cette première année : C1=
€
A l'aide des résultats précédent, compléter le tableau suivant :
 Les solutions proposées correspondent forcément aux réponses trouvées. Les solutions proposées correspondent forcément aux réponses trouvées.
| Capital en début d'année
en € | Intérêt
en € | Capital à la fin d'année
en € | | 1er année |
|
|
| | 2e année |
| | |
| ue année | | | |
Les intérêts simples sont donnés par la relation suivante :
Une ou plusieurs réponses précédentes sont fausses.
 L'erreur classique est de penser que la durée du placement est de 7 ans alors que pour la première année cette durée est de 1 an.
Vos réponses précédentes sont justes L'erreur classique est de penser que la durée du placement est de 7 ans alors que pour la première année cette durée est de 1 an.
Vos réponses précédentes sont justes
Le capital en début de 2e année a une valeur de €. ÉTAPE sur 5 Précisez les informations suivante : - La valeur du capital au début de la 2e année est de
€.
- Le taux annuel est de
.
 la valeur attendue ne doit pas être exprimée en pourcentage. la valeur attendue ne doit pas être exprimée en pourcentage. - La durée du placement de la deuxième année est de
an.
En utilisant la formule, déterminer les intérêts de la deuxième année : I=
€ En déduire le capital à la fin de cette deuxième année : C 2=
€ Compléter le tableau suivant :  Les solutions proposées correspondent forcément aux réponses trouvées. Les solutions proposées correspondent forcément aux réponses trouvées. | Capital en début d'année
en € | Intérêt
en € | Capital à la fin d'année
en € | | 1er année | | | | | 2e année | |
|
| | 3e année |
| | |
| ue année | | | |
Les intérêts simples sont donnés par la relation suivante :
Une ou plusieurs réponses précédentes sont fausses.
 La durée du placement est toujours de 1 an pour la deuxième année.
Vos réponses précédentes sont justes. La durée du placement est toujours de 1 an pour la deuxième année.
Vos réponses précédentes sont justes.
Le taux d'intérêt est de et la période est toujours de 1 an. ÉTAPE sur 5 Regarder la vidéo : Compléter le tableau : | Capital en début d'année
en € | Intérêt
en € | Capital à la fin d'année
en € |
| l année | | | |
| 3e année | |
|
|
| le année |
|
|
|
Conclusion : Le capital placé durant 7 années a une valeur actuelle de :
€. Le tableau réalisé évite les calculs fastidieux.
Une ou plusieurs réponses précédentes sont fausses. En effet les calculs sont interminables.
Vos réponses précédentes sont justes. Vous êtes un excellent calculateur.
Le tableau correct est le suivant : | Capital en début d'année
en € | Intérêt
en € | Capital à la fin d'année
en € |
| l année | | | |
En reprenant le tableau précédent, on a : | Capital |
C |
| Montant du capital en fin d'année | | | | | | | | | On passe d'un terme à l'autre en
la valeur
. Par conséquent les différents termes forment une suite
de premier terme
et de raison
. Afin d'éviter l'ensemble de ses calculs, une des deux formules sur les suites permet le calcul direct de la valeur acquise au bout de la septième année. Pour une suite arithmétique, la relation est donnée par :
| | Pour une suite géométrique, la relation est donnée par :
| | | |
raison =
n =
Un = U0 + n 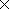 r r
Un =
+
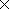
|  Choisir la bonne formule Choisir la bonne formule
et mettre la valeur x dans les cases de la formule non utilisée |
Un = U0 qn
Un =
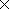
|
A l'aide de la calculatrice, on calcule : Un =
€ Conclusion : Le capital placé durant 7 années a une valeur acquise de :
€. Le calcul réalisé est rapide.
Conclusion : Le capital placé durant 7 années a une valeur acquise de : €. ÉTAPE sur 5 Par conséquent cliquez sur le bien de consommation que l'élève peut s'offrir :
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: le but des exercices est de déterminer les expressions d'une suite. exercises interactifs, calcul et tracé de graphes en ligne
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, sequence,arithmetic_sequence,geometric_sequence,Suite numérique,Suite arithmétique,Suite géométrique,Suite
| | | |



 Le calcul du quotient doit être arrondi à 10-4.
Le calcul du quotient doit être arrondi à 10-4. tm
tm